Nyquist Plot: What Is It? Stability Criteria and Key Terminologies

The Nyquist plot builds on polar plots to check the stability of closed-loop control systems by changing ω from −∞ to ∞. It shows the full frequency response of the open-loop transfer system. The Nyquist plot is a useful tool in control systems and signal processing for studying a system’s stability and frequency response. In this article, we will explain what a Nyquist plot is, its purpose, advantages, and disadvantages. This information will be very helpful in the Electrical field.

What is a Nyquist Plot?

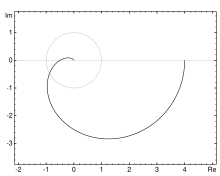
A Nyquist plot helps in control engineering and signal processing to check the stability of feedback systems. It shows the transfer function’s real part on the X-axis and the imaginary part on the Y-axis using Cartesian coordinates.

The plot changes as frequency varies, and you can also describe it in polar coordinates. In polar form, the radial coordinate represents the gain of the transfer function, while the angular coordinate shows its phase.

To analyze stability, you look at where the roots of the characteristic equation lie on the s-plane. A system stays stable if the roots are on the left side of the s-plane. Engineers use methods like the Nyquist plot, Nichols plot, and Bode plot to study relative stability.

The Nyquist stability criterion helps find where the roots of the characteristic equation are within a specific region of the s-plane. To understand a Nyquist plot, you first need to know some basic terms. For example, a closed path in a complex plane is called a contour.

Nyquist Stability Criteria

The Nyquist plot uses a simple graphical method called the Nyquist stability criterion to check system stability. To analyze the stability of a closed-loop system, you look at how the plot encircles the critical point (-1+j0). The rules are:

• No encirclement: The system is stable.
• Anticlockwise encirclement: The number of encirclements matches the number of system poles in the right half of the plane.
• Clockwise encirclement: The system is completely unstable.

This method gives a visual way to check stability without directly calculating poles. If the number of encirclements matches the number of right-half plane poles, the system is marginally stable.

Nyquist plots extend polar plots to analyze the stability of closed-loop control systems. Stability alone is not enough for practical systems. The system must also have stability margins that indicate how robust it is. Gain and phase margins are common ways to measure this, inspired by the Nyquist stability criterion.

Increasing the controller’s gain stretches the Nyquist plot outward, while increasing the controller’s phase twists the plot. By looking at the Nyquist plot, you can easily find how much gain or phase you can add before the system becomes unstable.

Nyquist Path or Nyquist Contour

The Nyquist path is a closed loop in the s-plane that covers the entire right-hand side. To do this, a large semicircular path is drawn with its diameter along the jω axis and its center at the origin. The radius of this semicircle is called the Nyquist Encirclement.

Nyquist Encirclement

A point lies inside a contour if the contour completely surrounds it.

Nyquist Mapping

Mapping means moving a point from the s-plane to the F(s) plane using the function F(s).

How to Draw Nyquist Plot in Simple Steps

Pros and Cons of Nyquist Plot

Pros

• Detailed Stability Check: It shows how stable a system is across all frequencies.
• Easy to Visualize: The graph format makes it simple to understand and evaluate system stability.
• Encirclement Count: You can easily count encirclements to check stability.
• Checks Robustness: It helps you find gain and phase margins, which are crucial for a system’s strong performance.

Cons

• Complex Math: Drawing a Nyquist plot requires a lot of mathematical work.
• Hard to Interpret: Understanding the plot can be tricky for systems with many poles and zeros.
• Frequency Coverage Issues: Covering the entire frequency range can be tough, especially for systems with high frequencies.

Key Terms in Nyquist Plot

To use the Nyquist plot effectively, it’s important to understand some key terms. Here are the main ones:

Nyquist Path or Contour

The Nyquist path (or contour) is the path traced by the frequency response of the open-loop transfer function in the complex plane. This path usually circles the entire right half of the s-plane.

Nyquist Encirclement

Nyquist encirclement refers to how many times the Nyquist path goes around the critical point (-1, 0). The direction (clockwise or counterclockwise) of these encirclements helps determine system stability.

Nyquist Mapping

Nyquist mapping involves plotting the frequency response of the open-loop transfer function on the complex plane. This helps visualize how the system behaves at different frequencies.

Gain Crossover Frequency

The gain crossover frequency is the frequency where the magnitude of the open-loop transfer function equals one (0 dB). This frequency is important for assessing the system’s phase margin.

Phase Crossover Frequency

The phase crossover frequency is the frequency where the phase angle of the open-loop transfer function reaches -180 degrees. This frequency is important for determining the system’s gain margin.

Phase Margin

Phase margin is the amount of additional phase lag needed to make the system unstable. It’s measured at the gain crossover frequency and is crucial for ensuring system stability.

Gain Margin

Gain margin is the amount of gain increase needed to make the system unstable. It’s measured at the phase crossover frequency and helps assess the system’s robustness.

Conclusion

The Nyquist plot is an essential tool for studying the stability of feedback systems. It clearly shows the frequency response on the complex plane, making it easy to understand. This simple yet powerful method is useful in various fields, including electrical, electronics, and control systems that involve feedback loops.

FAQs

What is a Nyquist plot?

A Nyquist plot is a graph that shows how feedback and gain relate in a feedback system, like an amplifier.

What are Nyquist and Bode plots?

Bode plots show a system’s frequency response with two plots: one for gain (magnitude) and one for phase. The Nyquist plot combines both gain and phase in a single complex graph.

What is a simple Nyquist plot?

To create a Nyquist plot, check the poles of G(s)H(s) on the jω axis, then choose the correct Nyquist contour, which includes the right half of the s-plane by drawing a large semicircle.

What is a Nyquist plot in electrochemistry?

In electrochemistry, Nyquist plots are used in electrochemical impedance spectroscopy (EIS) to represent the real and imaginary parts of complex impedance of electrodes for electrochemical cells.

Read More – What You Need To Know About Electric Poles