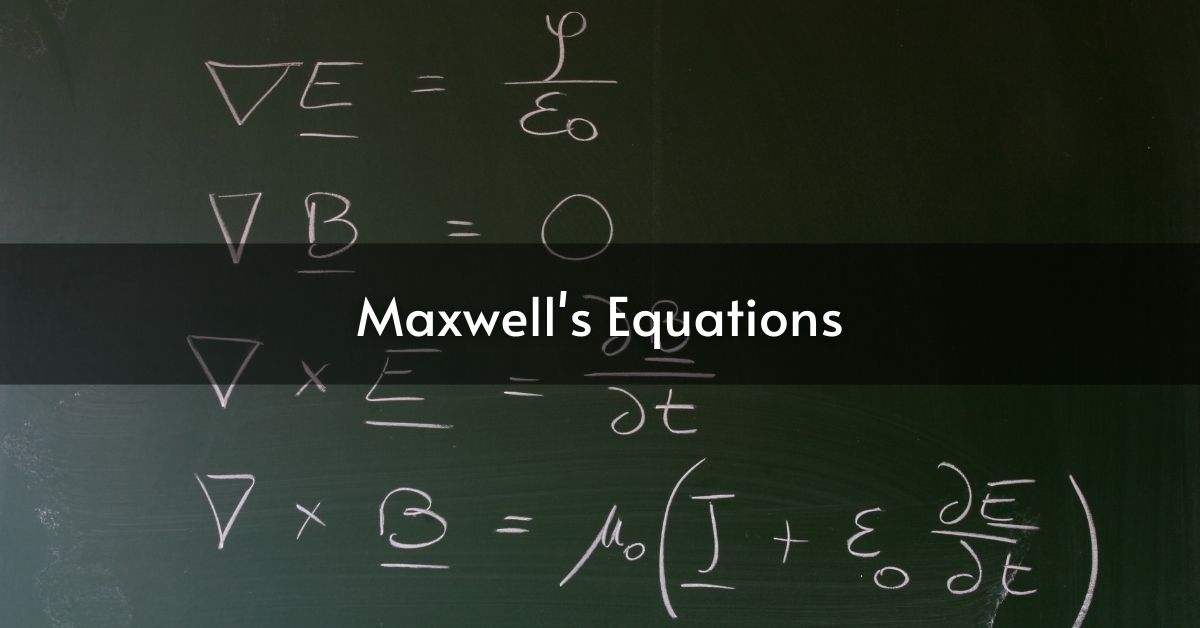Maxwell’s equations are the cornerstone of electromagnetism that provides the interplay between electric and magnetic fields. In this blog, we will concentrate specifically on Gauss’s Law for the electric field and elucidate it as comprehensively as possible. We would discuss both the differential and the integral expressions of this law so as to clarify the situational application of this law to particular phenomena.
The Importance of Maxwell’s Equations
Maxwell’s equations combine the ideas of electricity and magnetism in a simple, near-ideal way that supersedes nearly 100 years’ work by Coulomb, Gauss, Ampere, and Faraday. Nearly 200 years after these equations were born, they remain our best route to understanding the laws of the electromagnetic field and its carrier particle, the photon. Maxwell’s equations come in two varieties: differential and integral. Each is useful for different situations, and the differential form facilitates analysis over a localized interval whereas the integral form allows insight into an entire surface.
Gauss’s Law for the Electric Field
The first of Maxwell’s equations we will cover is Gauss’s Law for the electric field. Both of its forms have separate applications. The differential form is applied when seeking expressions that describe a certain condition, whereas the integral form applies when solving for something in a given region. The differential form is this: the divergence of the electric field in some region is proportional to charge density in that same region. Less technically, it describes how electric field lines diverge out from a point charge.
Differential Form of Gauss’s Law
The differential form of Gauss’s Law can be expressed mathematically as:
∇ • E = ρ / ε₀
Where:
- ∇ • E represents the divergence of the electric field.
- ρ is the charge density (charge per unit volume).
- ε₀ is the permittivity of free space.
This equation shows that the divergence of an electric field at a given point is proportional to the charge density at the same point. If there is a positive charge, the electric field lines will radiate outward, indicating a positive divergence. Conversely, if the charge was negative, then the field lines will converge inward and this implies negative divergence.
Integral Form of Gauss’s Law
The integral form of Gauss’s Law can be expressed as:
∮ E • da = Q_enc / ε₀
Where:
- ∮ E • da is the electric flux through a closed surface.
- Q_enc is the total charge enclosed within the surface.
This equation asserts that the total electric flux penetrating a closed surface is proportional to the charge lying within that surface. This form is extremely useful in calculations of the electric field created by symmetrical charge distributions, including spheres, cylinders, and planes.
Derivation of Gauss’s Law
To derive Gauss’s Law we start from its differential form, and integrate both sides over a volume. The divergence theorem helps to convert the volume integral of the divergence of the electric field into a surface integral.
After integrating both sides, we get the integral form that clearly shows how the electric field connects to the charge distribution inside a closed surface.
Applications of Gauss’s Law
Gauss’s Law is most useful under a condition of charge symmetry. It can be used for all kinds of calculations involving electric fields:
- Spherical Symmetry: For a uniformly charged sphere, the field outside is everywhere as if all the charge were concentrated at the center.
- Cylindrical Symmetry: The electric field far from the axis for an infinitely long charged cylinder is very easily calculated with Gauss’s Law.
- Planar Symmetry: The electric field in an infinite plane of charge is constant, and we can determine it by using Gauss’s Law, irrespective of the distance from the plane.
Understanding Charge Density
Charge density is the amount of charge per unit volume. How charge density relates to electric field strength is one important application of Gauss’s Law.
When the charge density is uniform, the electric field can be found directly from this charge distribution. However, when the charge distribution is not uniform, one must integrate over the charge density to find the electric field.
Challenges in Applying Gauss’s Law
Gauss’s Law is indeed a strong tool, but it may not be applied at times. It works the best in situations involving high symmetries. If the charge distributions are irregular or rather complex, then some other methods like Coulomb’s Law or numerical simulation can be used.
Moreover, Gauss’s Law fails to describe time-varying electric fields, which is the largest part of electrodynamics. The limitation demands understanding of the other Maxwell’s equations for embracing dynamic conditions.
Gauss’s Law in Electrostatics
Gauss’s Law is a natural choice for the analysis of electric fields when charges are stationary. Electrostatic problems are very intuitive and can have clearly defined boundary conditions.
The electric field problems, although common in practice, are normally problems with simple shapes. Maybe charged spheres or infinite sheets of charge are among them. These are configurations that by virtue of their symmetry, are easily treated using Gauss’s Law and which prove handy for physicists and engineers in practice.
Limitations of Maxwell’s Equations in Quantum Electrodynamics
Maxwell’s equations and the Lorentz force law (part of classical electromagnetism) work very well for explaining many phenomena. However, they do not include quantum effects, so they only apply in certain situations. People view Maxwell’s equations as the classical version of quantum electrodynamics (QED).
Some electromagnetic phenomena, like photon-photon scattering and quantum entanglement of electromagnetic fields, don’t fit with Maxwell’s equations. For example, quantum cryptography can’t be explained by Maxwell’s theory. As we deal with very strong electromagnetic fields or very small distances, the limits of Maxwell’s equations become clearer.
These equations of Maxwell can’t explain how a solitary photon interacts with quantum matter, such as in the photoelectric effect or Planck’s law, or within a single-photon detector.
Conclusion
In conclusion, Gauss’s Law for the electric field plays an important role in Maxwell’s equations. It helps explain how electric fields behave around different charges. By learning both the differential and integral forms of the law, physicists can solve many problems in electromagnetism. As we move forward with Maxwell’s equations, we will explore magnetism next, adding more to our understanding of this important topic. Keep an eye out for the next part, where we will discuss the magnetic side of Gauss’s Law and complete the static view of electromagnetism!
FAQs
What are electromagnetic waves?
Electromagnetic waves form when a magnetic field and an electric field vibrate together.
What do Maxwell’s equations explain?
They explain how electric charges and currents create magnetic and electric fields. They also show how an electric field can create a magnetic field and vice versa.
What does Maxwell’s third equation say?
Maxwell’s third equation says that a changing magnetic field always creates an electric field.
What is the formula for Gauss’ Magnetism Law?
The formula for Gauss’ Magnetism Law is: ∇. B = 0.
What is scalar electric flux?
Scalar electric flux refers to imaginary lines of force that spread outward from a source.
Read More – Power in Electrical Circuits: Understanding the Fundamentals