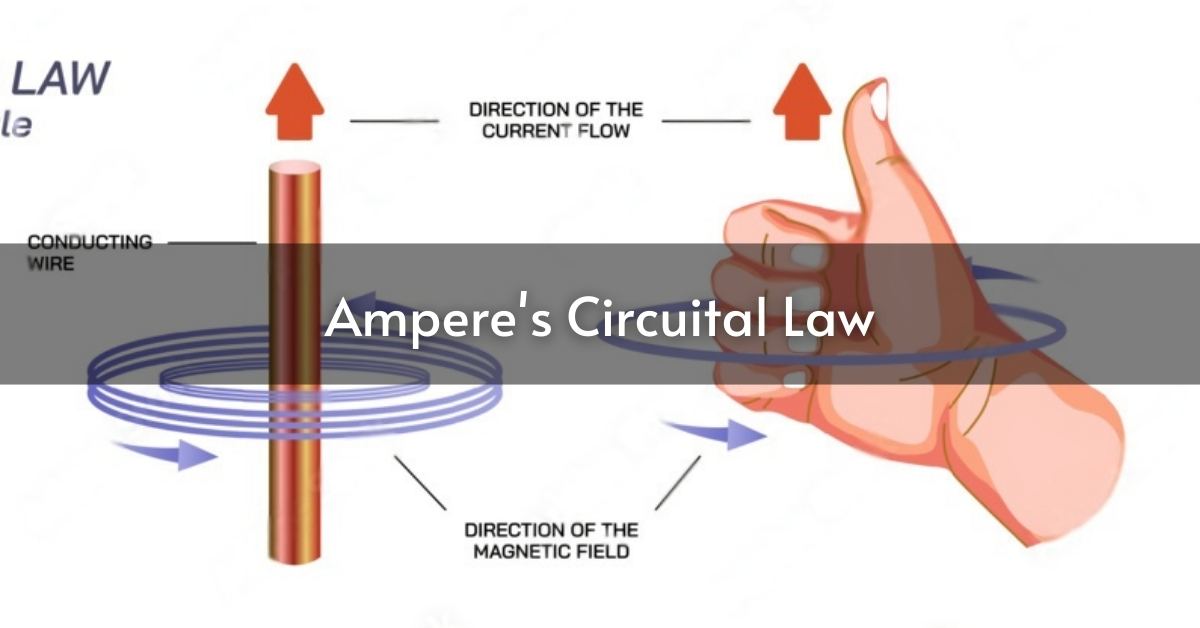
Ampere’s Circuital Law is one of the basic elements that predict the relation between electric currents and magnetic fields. For the students of physics, this law is important not only in higher studies but also while preparing for any type of competitive examination. Let us explore Ampere’s circuital law, its proof, and its applications in the following article. Who Was...
Subscribe to Read Full Engineering Publication
This verified technical document contains complete mathematical derivations, IS/NBC 2016 code references, equipment sizing schedules, and AutoCAD DWG blueprints.
Have Specific Equipment or Plant Capacities to Calculate?
Our AI Specialist can troubleshoot technical issues, calculate duct velocity, determine chiller load, or size cables specifically for "Ampere’s Circuital Law: Understanding the Principles and Applications".
popeye21834
Licensed Engineering ContributorChartered Senior MEP Engineer & Review Board Specialist with extensive design, testing, and commissioning field experience across commercial and industrial infrastructure.
Leave a Reply